Teknik Transmisi Telekomunikasi

Loncat ke navigasiLoncat ke pencarian

Transmisi merupakan sebuah pemancar (Transmitter) telekomunikasi yang bertujuan untuk memancarkan sinyal Radio Frekuensi (RF) yang membawa sinyal informasi berupa gambar (Video) dan suara (Audio), sehingga dapat diterima oleh pesawat penerima (Receiver) TV di daerah yang tercakup/tercover oleh pemancar TV tersebut.

Dalam rekayasa frekuensi radio , saluran transmisi adalah kabel khusus atau struktur lain yang dirancang untuk melakukan arus bolak-balik frekuensi radio , yaitu arus dengan frekuensi yang cukup tinggi sehingga sifat gelombangnya harus diperhitungkan. Saluran transmisi digunakan untuk tujuan seperti menghubungkan pemancar dan penerima radio dengan antena mereka (feed atau feeder), mendistribusikan sinyal televisi kabel , panggilan routing trunklines antara pusat-pusat switching telepon, koneksi jaringan komputer dan bus data komputer kecepatan tinggi.

Artikel ini mencakup saluran transmisi dua konduktor seperti saluran paralel ( saluran tangga ), kabel koaksial, stripline , dan microstrip . Beberapa sumber juga merujuk pada pandu gelombang , pandu gelombangdielektrik , dan bahkan serat optik sebagai saluran transmisi, namun saluran ini memerlukan teknik analitik yang berbeda sehingga tidak dicakup oleh artikel ini; lihat Waveguide (elektromagnetisme) .

Ikhtisar

Kabel listrik biasa cukup untuk membawa arus bolak-balik frekuensi rendah (AC), seperti daya listrik , yang membalikkan arah 100 hingga 120 kali per detik, dan sinyal audio . Namun, mereka tidak dapat digunakan untuk membawa arus dalam rentang frekuensi radio , di atas sekitar 30 kHz, karena energi cenderung memancarkan kabel sebagai gelombang radio , yang menyebabkan hilangnya daya. Arus frekuensi radio juga cenderung memantul dari diskontinuitas pada kabel seperti konektor dan sambungan, dan bergerak turun kembali ke arah sumber.  Refleksi ini bertindak sebagai hambatan, mencegah daya sinyal mencapai tujuan. saluran transmisi menggunakan konstruksi khusus, dan pencocokan impedansi , untuk membawa sinyal elektromagnetik dengan pantulan minimal dan kehilangan daya. Ciri pembeda dari sebagian besar saluran transmisi adalah bahwa mereka memiliki dimensi penampang yang seragam sepanjangnya, memberi mereka impedansi yang seragam, yang disebut impedansi karakteristik ,  untuk mencegah refleksi. Jenis-jenis saluran transmisi termasuk saluran paralel ( ladder line , twisted pair ), kabel coaxial , dan saluran transmisi planar seperti stripline dan microstrip .  Semakin tinggi frekuensi gelombang elektromagnetik bergerak melalui kabel atau media tertentu, semakin pendek panjang gelombang gelombang. Saluran transmisi menjadi perlu ketika panjang gelombang frekuensi yang ditransmisikan cukup pendek sehingga panjang kabel menjadi bagian penting dari panjang gelombang.

Pada frekuensi gelombang mikro dan di atasnya, daya yang hilang pada saluran transmisi menjadi berlebihan, dan sebagai gantinya, pandu gelombang digunakan,  yang berfungsi sebagai "pipa" untuk membatasi dan memandu gelombang elektromagnetik.  Beberapa sumber mendefinisikan pandu gelombang sebagai jenis saluran transmisi;  Namun, artikel ini tidak akan memasukkan mereka. Pada frekuensi yang bahkan lebih tinggi, dalam terahertz , inframerah dan rentang yang terlihat , pandu gelombang pada gilirannya menjadi lossy, dan metode optik , (seperti lensa dan cermin), digunakan untuk memandu gelombang 

Sejarah

Analisis matematis tentang perilaku saluran transmisi listrik muncul dari karya James Clerk Maxwell , Lord Kelvin dan Oliver Heaviside . Pada tahun 1855 Lord Kelvin merumuskan model difusi arus dalam kabel bawah laut. Model ini dengan benar memprediksi kinerja buruk kabel telegraf kapal selam trans-Atlantik 1858. Pada tahun 1885 Heaviside menerbitkan makalah pertama yang menggambarkan analisisnya tentang propagasi dalam kabel dan bentuk modern dari persamaan telegrapher.

Empat Model Terminal[sunting | sunting sumber]

Variasi pada simbol elektronik skematis untuk saluran transmisi

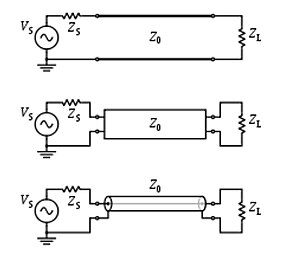
Untuk keperluan analisis, saluran transmisi listrik dapat dimodelkan sebagai jaringan dua-port (juga disebut quadripole), sebagai berikut:

Dalam kasus yang paling sederhana, jaringan diasumsikan linier (yaitu tegangan kompleks di kedua port sebanding dengan arus kompleks yang mengalir ke dalamnya ketika tidak ada pantulan), dan kedua port diasumsikan dapat dipertukarkan. Jika saluran transmisi seragam sepanjang, maka perilakunya sebagian besar dijelaskan oleh parameter tunggal yang disebut impedansi karakteristik , simbol Z0. Ini adalah rasio dari tegangan kompleks dari gelombang yang diberikan ke arus kompleks dari gelombang yang sama di setiap titik di saluran. Nilai tipikal Z ₀ adalah 50 atau 75 ohm untuk kabel koaksial , sekitar 100 ohm untuk pasangan kabel bengkok, dan sekitar 300 ohm untuk jenis umum pasangan tidak berpilin yang digunakan dalam transmisi radio.

Saat mengirimkan daya ke saluran transmisi, biasanya diinginkan bahwa daya sebanyak mungkin akan diserap oleh beban dan sesedikit mungkin akan dipantulkan kembali ke sumbernya. Ini dapat dipastikan dengan membuat impedansi beban sama dengan Z ₀ , dalam hal ini saluran transmisi dikatakan cocok .

Saluran transmisi diambil sebagai dua kabel hitam.Pada jarak x ke saluran, ada arus I(x) yang berjalan melalui masing-masing kabel, dan ada perbedaan tegangan V(x) antara kabel. Jika arus dan tegangan berasal dari gelombang tunggal (tanpa refleksi), maka V(x) / I(x) = Z ₀ , di mana Z ₀ adalah impedansi karakteristik saluran.

Beberapa daya yang dimasukkan ke dalam saluran transmisi hilang karena hambatannya.Efek ini disebut kerugian ohmik atau resistif (lihat pemanasan ohmik ). Pada frekuensi tinggi, efek lain yang disebut kerugian dielektrik menjadi signifikan, menambah kerugian yang disebabkan oleh resistensi. Kehilangan dielektrik disebabkan ketika bahan isolasi di dalam saluran transmisi menyerap energi dari medan listrik bolak-balik dan mengubahnya menjadi panas (lihat pemanasan dielektrik ). Saluran transmisi dimodelkan dengan resistansi (R) dan induktansi (L) secara seri dengan kapasitansi (C) dan konduktansi (G) secara paralel.Hambatan dan konduktansi berkontribusi terhadap hilangnya saluran transmisi.

Kehilangan total daya dalam saluran transmisi sering ditentukan dalam desibel per meter (dB / m), dan biasanya tergantung pada frekuensi sinyal. Pabrikan sering menyediakan bagan yang menunjukkan kerugian dalam dB / m pada rentang frekuensi. Hilangnya 3 dB kira-kira setara dengan separuh dari daya.

Saluran transmisi frekuensi tinggi dapat didefinisikan sebagai saluran yang dirancang untuk membawa gelombang elektromagnetik yang panjang gelombangnya lebih pendek dari atau sebanding dengan panjang saluran. Dalam kondisi ini, perkiraan yang berguna untuk perhitungan pada frekuensi yang lebih rendah tidak lagi akurat. Ini sering terjadi pada sinyal radio,microwave,optik,filter optik mesh logam, dan dengan sinyal yang ditemukan di sirkuit digital berkecepatan tinggi.

Persamaan Telegrapher[sunting | sunting sumber]

Persamaan telegrapher (atau hanya persamaan telegraf ) adalah sepasang persamaan diferensial linier yang menggambarkan tegangan (V) dan arus (I) pada saluran transmisi listrik dengan jarak dan waktu. Mereka dikembangkan oleh Oliver Heaviside yang menciptakan model saluran transmisi , dan didasarkan pada Persamaan Maxwell.

Representasi skematik dari komponen dasar saluran transmisi.

Model saluran transmisi adalah contoh dari model elemen terdistribusi . Ini mewakili saluran transmisi sebagai rangkaian tak terbatas dari komponen dasar dua-port, masing-masing mewakili segmen pendek yang sangat pendek dari saluran transmisi:

• Resistansi R didistribusikan konduktor diwakili oleh resistor seri (dinyatakan dalam ohm per satuan panjang).

• Induktansi  L didistribusikan (karena medan magnet di sekitar kabel, induktansi sendiri , dll.) diwakili oleh induktor seri (dalam henries per satuan panjang).

• Kapasitansi  C antara dua konduktor diwakili oleh kapasitor shunt (dalam farad per satuan panjang).

• Konduktansi  G dari bahan dielektrik yang memisahkan dua konduktor diwakili oleh resistor shunt antara kabel sinyal dan kabel kembali (dalam siemens per satuan panjang).

Model terdiri dari serangkaian elemen tak terbatas yang ditunjukkan pada gambar, dan nilai-nilai komponen ditentukan per satuan panjang sehingga gambar komponen dapat menyesatkan R,L,C dan G mungkin juga merupakan fungsi frekuensi. Notasi alternatif adalah menggunakan  R',L',C' dan G' untuk menekankan bahwa nilai adalah turunan sehubungan dengan panjang. Kuantitas ini juga dapat dikenal sebagai konstanta saluran primer untuk membedakan dari konstanta saluan sekunder yang diturunkan darinya, ini adalah konstanta propagasi , konstanta atenuasi dan konstanta fasa.

Tegangan saluran V(x) dan arus I(x) dapat dinyatakan dalam domain frekuensi sebagai

${\displaystyle {\displaystyle {\frac {\partial V(x)}{\partial x}}=-(R+j\,\omega \,L)\,I(x)}}$

${\displaystyle {\displaystyle {\frac {\partial I(x)}{\partial x}}=-(G+j\,\omega \,C)\,V(x)~\,.}}$

Kasus Khusus dari Saluran Tanpa Kerugian[sunting | sunting sumber]

Ketika elemen R dan G sangat kecil saluran transmisi dianggap sebagai struktur lossless.  Dalam kasus hipotetis ini, model hanya bergantung pada L dan C elemen yang sangat menyederhanakan analisis. Untuk saluran transmisi lossless, persamaan Telegrapher kondisi tunak orde kedua adalah:

${\displaystyle {\displaystyle {\frac {\partial ^{2}V(x)}{\partial x^{2}}}+\omega ^{2}L\,C\,V(x)=0}}$

${\displaystyle {\displaystyle {\frac {\partial ^{2}I(x)}{\partial x^{2}}}+\omega ^{2}L\,C\,I(x)=0~\,.}}$

Ini adalah persamaan gelombang yang memiliki gelombang bidang dengan kecepatan rambat yang sama di arah maju dan mundur sebagai solusi. Signifikansi fisik dari hal ini adalah bahwa gelombang elektromagnetik merambat ke bawah saluran transmisi dan secara umum, ada komponen yang dipantulkan yang mengganggu sinyal asli. Persamaan ini dasar untuk teori saluran transmisi.

Kasus Umum dari Sebuah Saluran dengan Kerugian[sunting | sunting sumber]

Dalam kasus umum ketentuan kerugian, R dan G , keduanya disertakan, dan bentuk lengkap persamaan Telegrapher menjadi:

${\displaystyle {\displaystyle {\frac {\partial ^{2}V(x)}{\partial x^{2}}}=\gamma ^{2}V(x)\,}}$

${\displaystyle {\displaystyle {\frac {\partial ^{2}I(x)}{\partial x^{2}}}=\gamma ^{2}I(x)\,}}$

Dimana  ${\displaystyle {\displaystyle \gamma }}$ adalah konstanta propagasi ( kompleks ). Persamaan ini dasar untuk teori saluran transmisi. Mereka juga persamaan gelombang , dan memiliki solusi yang mirip dengan kasus khusus, tetapi merupakan campuran sinus dan cosinus dengan faktor peluruhan eksponensial. Pemecahan untuk konstanta propagasi ${\displaystyle {\displaystyle \gamma }}$ dalam hal parameter primer R,L,Gdan C diberikan:

${\displaystyle {\displaystyle \gamma ={\sqrt {(R+j\,\omega \,L)(G+j\,\omega \,C)\,}}}}$

dan impedansi karakteristik dapat dinyatakan sebagai

${\displaystyle {\displaystyle Z_{0}={\sqrt {{\frac {R+j\,\omega \,L}{G+j\,\omega \,C}}\,}}~\,.}}$

Solusi untuk V(x) dan I(x) adalah:

${\displaystyle {\displaystyle V(x)=V_{(+)}e^{-\gamma \,x}+V_{(-)}e^{+\gamma \,x}\,}}$

${\displaystyle {\displaystyle I(x)={\frac {1}{Z_{0}}}\,\left(V_{(+)}e^{-\gamma \,x}-V_{(-)}e^{+\gamma \,x}\right)~\,.}}$

Konstanta ${\displaystyle {\displaystyle V_{(\pm )}}}$ harus ditentukan dari kondisi batas. Untuk tegangan pulsa  ${\displaystyle {\displaystyle V_{\mathrm {in} }(t)\,}}$, mulai dari ${\displaystyle {\displaystyle x=0}}$dan bergerak pada arah ${\displaystyle {\displaystyle x}}$ positif, kemudian pulsa yang dikirim  pada posisi ${\displaystyle {\displaystyle x}}$dapat diperoleh dengan menghitung Transformasi Fourier, ${\displaystyle {\displaystyle {\tilde {V}}(\omega )}}$dari ${\displaystyle {\displaystyle V_{\mathrm {in} }(t)\,}}$  , menipiskan setiap komponen frekuensi dengan${\displaystyle {\displaystyle e^{-\operatorname {Re} (\gamma )\,x}\,}}$, memajukan fase dengan ${\displaystyle {\displaystyle -\operatorname {Im} (\gamma )\,x\,}}$, dan mengambil Fourier Transform terbalik . Bagian nyata dan imajiner dari ${\displaystyle {\displaystyle \gamma }}$ dapat dihitung sebagai

${\displaystyle {\displaystyle \operatorname {Re} (\gamma )=\alpha =(a^{2}+b^{2})^{1/4}\cos(\psi )\,}}$

${\displaystyle {\displaystyle \operatorname {Im} (\gamma )=\beta =(a^{2}+b^{2})^{1/4}\sin(\psi )\,}}$

dengan

${\displaystyle {\displaystyle a~\equiv ~R\,G\,-\omega ^{2}L\,C\ ~=~\omega ^{2}L\,C\,\left[\left({\frac {R}{\omega L}}\right)\left({\frac {G}{\omega C}}\right)-1\right]}}$

${\displaystyle {\displaystyle b~\equiv ~\omega \,C\,R+\omega \,L\,G~=~\omega ^{2}L\,C\,\left({\frac {R}{\omega \,L}}+{\frac {G}{\omega \,C}}\right)}}$

rumus ruas kanan digunakan ketika tidak ada L, juga tidak C juga tidak ${\displaystyle {\displaystyle \omega }}$adalah nol, dan dengan

${\displaystyle {\displaystyle \psi ~\equiv ~{\tfrac {1}{2}}\operatorname {atan2} (b,a)\,}}$

di mana atan2 adalah bentuk fungsi dua-parameter arctan yang didefinisikan di mana-mana, dengan nilai arbitrer nol ketika kedua argumen adalah nol.

Khusus, Kasus Kerugian Rendah[sunting | sunting sumber]

Untuk kerugian kecil dan frekuensi tinggi, persamaan umum dapat disederhanakan: Jika ${\displaystyle {\displaystyle {\tfrac {R}{\omega \,L}}\ll 1}}$dan  ${\displaystyle {\displaystyle {\tfrac {G}{\omega \,C}}\ll 1}}$kemudian

${\displaystyle {\displaystyle \operatorname {Re} (\gamma )=\alpha \approx {\tfrac {1}{2}}{\sqrt {L\,C\,}}\,\left({\frac {R}{L}}+{\frac {G}{C}}\right)\,}}$

${\displaystyle {\displaystyle \operatorname {Im} (\gamma )=\beta \approx \omega \,{\sqrt {L\,C\,}}~.\,}}$

Memperhatikan bahwa kemajuan dalam fase oleh ${\displaystyle {\displaystyle -\omega \,\delta }}$ setara dengan penundaan waktu oleh ${\displaystyle {\displaystyle \delta }}$, ${\displaystyle {\displaystyle V_{out}(t)}}$ dapat dengan mudah dihitung dengan

${\displaystyle {\displaystyle V_{\mathrm {out} }(x,t)\approx V_{\mathrm {in} }(t-{\sqrt {L\,C\,}}\,x)\,e^{-{\tfrac {1}{2}}{\sqrt {L\,C\,}}\,\left({\frac {R}{L}}+{\frac {G}{C}}\right)\,x}.\,}}$